Latex-katex-test

At first, we sample f(x) in the N ( N is odd) equidistant points around x^* :
f_k = f(x_k),\: x_k = x^*+kh,\: k=-\frac{N-1}{2},\dots,\frac{N-1}{2}

where h is some step.

Then we interpolate points \{(x_k,f_k)\} by polynomial
P_{N-1}(x)=\sum_{j=0}^{N-1}{a_jx^j}
Its coefficients \{a_j\} are found as a solution of system of linear equations:
\left\{ P_{N-1}(x_k) = f_k\right\},\quad k=-\frac{N-1}{2},\dots,\frac{N-1}{2}

Autre essai

Une formule simple : y=R^{-1}\cdot x en ligne

Une formule avec matrice en ligne : 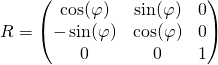 R=\begin{pmatrix}\cos(\varphi) & \sin(\varphi) & 0\\ -\sin(\varphi) & \cos(\varphi) & 0\\ 0 & 0 & 1 \end{pmatrix}
La même hors ligne : 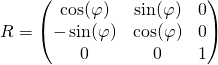 R=\begin{pmatrix}\cos(\varphi) & \sin(\varphi) & 0\\ -\sin(\varphi) & \cos(\varphi) & 0\\ 0 & 0 & 1 \end{pmatrix}

Une formule plus compliquée hors ligne

\dot{R}=\begin{pmatrix}-\sin(\varphi) & \cos(\varphi) & 0\\ -\cos(\varphi) & -\sin(\varphi) & 0\\ 0 & 0 & 0 \end{pmatrix}\cdot\dot{\varphi}=\begin{pmatrix}0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}\begin{pmatrix}\cos(\varphi) & \sin(\varphi) & 0\\ -\sin(\varphi) & \cos(\varphi) & 0\\ 0 & 0 & 1 \end{pmatrix}\cdot\dot{\varphi}

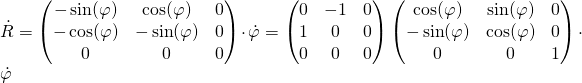
avec des matrices (dérivée d’une rotation d’angle : \varphi)

\begin{equation} pas reconnu